Lecture 5: predicate logic

javaIsTheBest

Question Source:

https://www.students.cs.ubc.ca/~cs-121/2017W2/slides/PredicateLogic-4up.pdf
https://www.students.cs.ubc.ca/~cs-121/2018S/slides/121-06-pred-logic-intro-ckh4up.pdf

Feel free to post question if you find any mistakes in the notes.

Q1
Which of the following placements of parentheses , yields the same meaning as:
∀x∈ Z, ∃y ∈ Z, x < y ∧ Even(y) ?
a) (∀ x∈ Z), ∃y ∈ Z, x < y ∧ Even(y)
b) (∀ x ∈ Z, ∃y ∈ Z, x < y) ∧ Even(y)
c) (∀x ∈ Z, ∃y ∈ Z, x < y ∧ Even(y))
d) None of the above.

notes:
a) there is no saying: (∀ x∈ Z)
b) A quantifier applies to everything to its right until a closing parenthesis stops it.
For the above question, without parenthesis ∀x∈ Z, ∃y ∈ Z will applies to the whole statement.
(∀ x ∈ Z, ∃y ∈ Z, x < y) ∧ Even(y) will make y in Even(y) unbounded
c) c is equivalent

Q2
Which of the following placements of parentheses yields the same meaning as:
~ ∃x∈ Z^+, ∃y ∈ Z^+, x < y ∧ Even(y)
a) (~ (∃x∈ Z⁺)), ∃y ∈ Z^+, x < y ∧ Even(y)
b) (~ (∃x∈ Z⁺)), ∃y ∈ Z^+, x < y ∧ Even(y)
c) (~ (∃x∈ Z^+, ∃y ∈ Z^+, x < y)) ∧ Even(y)
d) (~ (∃x∈ Z^+, ∃y ∈ Z^+, x < y ∧ Even(y)))
d) None of the above.

notes:
The answer would be d). The logic is the same as question 1.
The ~ applies to the whole statement.

Q3
What is the difference between a proposition and a predicate?
a) A predicate may contain one or more quantifiers, but a proposition never does.
b) A proposition's name is a lowercase letter, whereas a predicate's name is an uppercase letter.
c) A predicate may contain unbound variables, but a proposition does not.
d) They are the same thing, using different names.
e) None of the above.

notes:
Example: Perfect Square(y): ∃x ∈ Z, x * x = y
a) PerfectSquare(25)[∃ x ∈ Z, y = 25, x * x = y] is a proposition. It has quantifier ∃ x ∈ Z
b) PerfectSquare(25)[∃ x ∈ Z, y = 25, x * x = y] is a proposition, it uses uppercase letter
c) ∃y ∈ Z, PerfectSquare(y) is predicate and it is not a proposition.
More examples:
• Q(x, y) has two unbound variables (x and y), and is not a proposition.
• Q(1, y) = 1 + y > 2 [Not a proposition] one bound variable (x = 1) and one unbound variable (y).
• Q(1, 2) = 1 + 2 > 2 [Proposition] two bound variables (x = 1 and y = 2)
a proposition does not contain unbound variables, c) is correct.

Q4
Given the definitions:
F(x): x is a fierce creature.
L(x): x is a lion
C(x): x drinks coffee
D: the set of all creatures.
T(x,y): creature x has “tasted” creature y.

Express these statements using predicate logic:
(a)All lions are fierce.
(b)Some lions do not drink coffee.
(c)Some creature drinks coffee
(d)Some lion drinks coffee
(e)Some fierce lion drinks coffee
(f)Every creature drinks coffee
(g)Every lion drinks coffee
(h)Every fierce lion drinks coffee
(i)All fierce creatures are not lions.
aaGive two different (not logically equivalent),
aatranslations into predicate logic.
(j)Express these two propositions in English:
1.∀x ∈ D, ∃y ∈ D, T(x,y)
2.∃y ∈ D, ∀x ∈ D, T(x,y)
(k)There is exactly one creature drinks coffee
(l)There is at most one creature drinks coffee
(o)There are at least two creatures drink coffee

notes:
(a)∀ x∈ D, L(x) -> F(x)
(b)∃ x∈ D, L(x) ∧ ~ C(x)
(c)∃ x∈ D, C(x)
(d)∃ x∈ D, L(x) ∧ C(x)
(e)∃ x∈ D, L(x) ∧ F(x) ∧ C(x)
(f)∀ x∈ D, C(x)
(g)∀ x∈ D, L(x) -> C(x)
(h)∀ x∈ D, (L(x) ∧ F(x))-> C(x)
(i)1. All fierce creatures (that) are not lions ∀ x∈ D, ~ L(x) ∧ F(x)
aa2.All fierce creatures are not lions ∀ x∈ D, F(x) -> L(x)
(j)1. For all creatures, they has tasted at least one (other) creature.
aa2.There exists creatures that have been tasted by all creatures
(k)∃ x∈ D, C(x) ∧ ~ ∃ y∈ D, x =/= y ∧ C(y)
(l)~ ∃ x∈ D, ∃ y∈ D, x =/= y ∧ C(x) ∧ C(y)
(o)∃ x∈ D, ∃ y∈ D, x =/= y ∧ C(x) ∧ C(y)
summary

Q5
Assume that L represents a list of values.
The length of L is denoted by (length L).
The ith element of L is denoted by (list-ref L i).
The first element of L is (list-ref L 0).
Problem:
Define a predicate Sorted(L) whose value is true if and only if L is sorted in non-decreasing order. We can use the functions length and list-ref.

Q5(a)Which of the following is/are a problem with this definition?
Sorted(L) ≡ i ∈ N , j ∈ N, (list-ref L i) ^ (list-ref L j) ^ v_i < v_j
a) There is no quantifier for L.
b) There are no quantifiers for v_i and v_j
c) We can not use ^ with (list-ref L i) and (list-ref L j)
d) Both (a) and (b)
e) Both (b) and (c)
notes:
(b) and (c) are both problems.
v_i < v_j are not defined.
(list-ref L i) is a value, for example we cant say 3 ^ 4

Q5(b)Which of the following is/are a problem with this definition?
Sorted(L) ≡ i ∈ N , j ∈ N , i < j →(list-ref L i) < (list-ref L j)
a) It is too restrictive (it does not allow for equal values).
b) It does not restrict the ranges of i and j.
c) It is missing quantifiers.
d) Both (a) and (b)
e) Both (b) and (c)
notes:
Both (a) and (b) are problems.
It should include the equal case and i and j should be less than the length(L)

Combined 5(a) and 5 (b)
The predicate will be
Sorted(L) ≡ i ∈ N , j ∈ N , i < j < length(L) →(list-ref L i) <= (list-ref L j)

Q6 Efficiency of Algorithms
Let’s say each student is in a 1st year orientation group.
For each of their groupmates, each student has a list of all of their classes.
Assume each group has 13 students and each student is taking 5 classes.
I want to determine how many students in my class have a group mate in my class.

Which algorithm is generally faster?
(a) Ask each student for the list of their group mates’ classes, and check for each
class whether it is CPSC 121. If the answer is ever yes, include the student in my count.
(b) For each student s1 in the class, ask the student for each other student s2 in the
class whether s2 is a group mate. If the answer is ever yes, include s1 in my count

Say checking if a class on a list is CPSC121 takes 1 second and
checking if a classmate is in your group takes 1 second.

notes:
Assume there three student in class(A B and C)

In method 1, A has to check for the other 12 students' class list and every has
five course, so the time for A to check with his group is 12 * 5. And same for B
and C. So the time spent is 3 * 12 * 5 = 180 second

In method 2, A check with B and C if they are in the same group, which takes 2 seconds.
Same for B and C. So the time spent is 3 * 2 * 1 = 6 second.

Scale up the number of students and see what happen.
10 students：
(1) 10 * 12 * 5 = 10 minutes
(2) 10 * 9 * 1 = 1.5 minutes

100 students：
(1) 100 * 12 * 5 = 100 minutes
(2) 100 * 99 * 1 = 131 minutes

400 students：
(1) 400 * 12 * 5 = 400 minutes
(2) 400* 399 * 1 = 2660 minutes
...

n students：
(1) n* 12 * 5 = 60n seconds
(2) 400* 399 * 1 = n(n -1) seconds

We find out as n becomes larger, method 2's time spent will increase lot more faster than method 1

Q7 big(O)
As we can see from Q6, constant doesn't matter in terms of time spent as n becomes large enough.
So, we want to come up with a way to count steps that ignores these constants.
Terminology: an algorithm runs in O(g) time,stated “big-Oh of g time”, if it performs at most g(n) steps (approximately).
** f is in O(g) if ∃c ∈ R^+, ∃n₀ ∈ N, ∀n ∈ N, n ≥ n₀ → f(n) ≤ cg(n)
In English : f is in O(g) if there exists positive constants c and n₀ such that f (n) ≤ cg(n) for all n ≥ n_0.**

Q7(a)

notes:
From the definition, we knows that n₀ should be described. n ≥ n_0, means after some n₀ value,
f (n) is no more faster than cn² . So we choose (e)

Q7(b)
Is the following predicate true for f(n) = n?
∃c ∈ R^+, ∃n₀ ∈ N, ∀n ∈ N, n ≥ n₀ → f(n) ≤ cnlog₂ n
a) Yes
b) No
notes:
we can choose c = 1 , n₀ = 2 and substitute c in (f(n) ≤ cnlog₂ n)
n ≤ nlog₂ n ? as (n ≥ n₀ ≥ 2).
cancel n both sides, 1 <= log₂ n as (n ≥ n₀ ≥ 2) ? Yes

Q7(c)
Revisiting sorted lists:
Recall
Sorted(L) ≡ ∀ i ∈ N, ∀ j ∈ N, (0 ≤ i) ^ (i < j) ^ (j < (length L)) → (list-ref L i) ≤ (list-ref L j)
If we verify that L is sorted using this definition, how
many comparisons will we need?
notes:

consider an array of elements 5 6 7 8 9
according to this algorithm, 
for 5, it has to be compared with 6 7 8 9   (4 comparison)
for 6, it has to be compared with   7 8 9   (3 comparison)
for 7, it has to be compared with     8 9   (2 comparison)
for 8, it has to be compared with       9   (1 comparison)
for a general n, the total time is (n - 1) + (n -2) + .... 3 + 2 + 1 = (n-1)n/2
(n-1)n/2 ≤ cn^2
   n - 1 ≤ cn
       n ≤ cn + 1 we can choose c = 1, n0 = 1, then (n-1)n/2 is O(n^2)
(f is in O(g) if ∃c ∈ R^+, ∃n~0 ∈ N, ∀n ∈ N, n ≥ n~0 → f(n) ≤ cg(n))

Q7(d)
Revisiting sorted lists:
Recall
Sorted(L) ≡ ∀ i ∈ N, (0 ≤ i) ^ (i < (length L) - 1) → (list-ref L i) ≤ (list-ref L i+1)
If we verify that L is sorted using this definition, how
many comparisons will we need?
notes:

consider an array of elements 5 6 7 8 9
We check 5 6,
then     6 7,
then     7 8,
then     8 9.
Total is 4 times,
For a general is (n - 1) comparisons
n - 1 ≤ cn
    n ≤ cn + 1 we can choose c = 1, n0 = 1, then (n-1) is O(n)
(f is in O(g) if ∃c ∈ R^+, ∃n~0 ∈ N, ∀n ∈ N, n ≥ n~0 → f(n) ≤ cg(n))

We can see Q7(d)(O(n²)) is increasing faster than Q7(c)(O(n)).
In other way, Q7(d) is slower than Q7(c)
Some big(o) function comparison

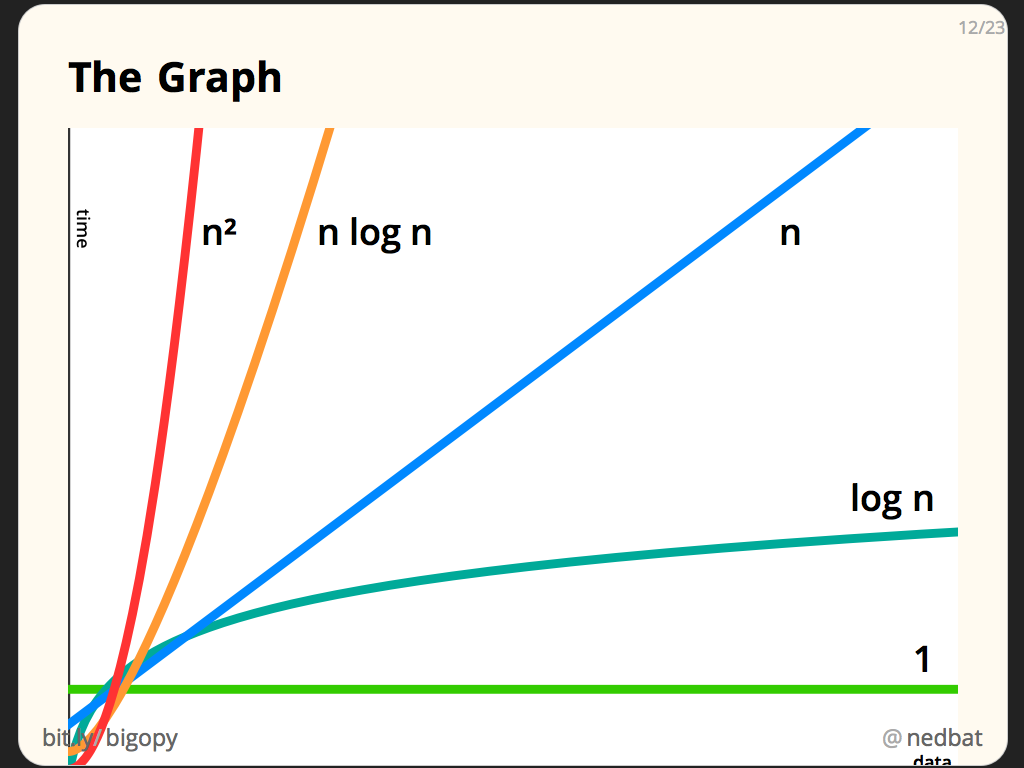
Q8 practice
Translate “returns true if and only if either l and x
are both equal to null, or l contains at least one
element e that is equal to x.
notes:

C(L, x): List L contains element x
N(x): x is null
E(x1, x2): x1 equals x2
C(L, x) ≡ (∃i ∈ N,(0 ≤ i) ^ (i < (length L) - 1) ^ E((list-ref L i), x)) v (N(L) ^ N(X))

Q9 practice
Define a predicate Prime(x) that evaluates to
true if and only if x is a prime. Assume that you
have a predicate | such that x | y is true if and
only if x divides y (that is, y/x is an integer).
notes:

prime(x) ≡ ~ Ey ∈ N,(y != 1) ^ (y != x) ^ (x | y)