Q1. 2018S/slides/121-02-prop-logic-ckh.pdf:page 19

I think all of the three are good. True table for all 3
#1 #2 #3
input output input output input output
0 0 0 1 0 0
1 1 1 0 1 1
As we can see, whenever we change the input, the light state changed
-
Q2. 2018S/slides/121-02-prop-logic-ckh.pdf:page 22

True table for all 3
#1(s1 ⊕ s2) #2(s1 ^ s2) #3(s2∧ ∼s1) ∨ (∼s1 ∧ s2)
s1 s2 output s1 s2 output s1 s2 output
0 0 0 0 0 0 0 0 0
0 1 1 0 1 0 0 1 1
1 0 1 1 0 0 1 0 1
1 1 0 1 1 1 1 1 0
For #1 and #3, as true table shows, change of s1 or s2 makes the light state changed.
For #2, say we change s1 = 0 , s2 = 0 to s1 = 0 , s2 = 1, the output is still 0, so #2 is incorrect
Actually, #1 and #3 are equivalent, reference formula sheet
s1 ⊕ s2
=(∼s1 ∧ s2) ∨ (s2 ∧ ∼s1) ;; [p ⊕ q ≡ (p∧ ∼q) ∨ (∼p ∧ q)]
=(s2 ∧ ∼s1) ∨ (∼s1 ∧ s2) ;; Commutative: [COM] p ∨ q ≡ q ∨ p
-
Q3. 2018S/slides/121-02-prop-logic-ckh.pdf:page 26

For b, we can directly tell it is wrong. Lets assume s1 = 1, s2 = 0 and s3 = 1 then output is 1.
if we change s2 to 1, the output is still 1. So, b is incorrect.
For the other options, actually they are equivalent.
reference formula sheet
p ⊕ q ≡ (p∧ ∼q) ∨ (∼p ∧ q)
s1 ⊕ (s2 ⊕ s3)
=(s1 ∧ ~(s2 ⊕ s3)) ∨ (~s1 ∧ (s2 ⊕ s3)) which is d
for proof (c) = (a)
Can reference this file
In this file, + menas ∨, · means ∧
For n switches of this question, we can implement a circuit using xor (s1 ⊕ (s2 ⊕ (s3 ⊕ ....(Sn-1⊕ Sn))))
-
Q4. 2018S/slides/121-02-prop-logic-ckh.pdf:page39
A circuit that displays the numbers 0 through 9 using seven LEDs.
What’s the circuit the lower-left segment e?
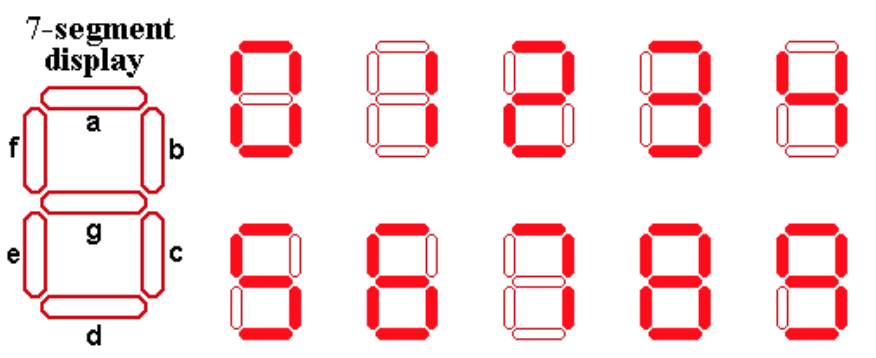
One bit(switch) can represent two states 0 and 1
Two bits can represent 4 states 00 01 10 and 11.
So n bits can represent 2n states.
Since there are 10 numbers (0 to 9), the least bits we need to represent 10 states is 4(24 = 16)

if we have the number representation with states like the above table.
We know that the segment e should be on only when number is 0 2 6 8.
So we can collect the 4 cases with the universality expression (collect all true cases)
(~a ∧ ~b ∧ ~c ∧ ~d) ∨(~a ∧ ~b ∧ c ∧~d) ∨ (~a ∧ b ∧ c ∧ ~d) ∨ ( a ∧ ~b ∧ ~c ∧ ~d)
If we want to simplify, we can use Karnaugh Maps method.

(Note: The 'X' mark means impossible case, we can view it as 1 for combination)
With the expression, we can build the circuit for e.
e = b'd' + cd' = (b' + c)d' = (~b ∨ c ) ∧ ~d

Using the same strategy for the rest segments(a, b, c, d, f, g), we can build the whole circuit
-
Q5. 2018S/slides/121-03-cond-equiv-ckh4up.pdf:page21


We can tell from the graph that the upper bar is only one when number is 4 5 6 7 8 9. We can by negating statement we construct! Instead of building out, we build (0 1 2 3) and then negate it ~ (0 v 1 v 2 v 3)
when we look at the true table for (0 1 2 3), we can simplify the expression
a b c d 'is ~, near means ∧, + means v
0 F F F F a'b'c'd' + a'b'c'd + a'b'cd' + a'b'cd
1 F F F T =a'b'(c'd' + c'd + cd' + cd)
2 F F T F =a'b'(c'(d' + d )+ c(d' + d))
3 F F T T =a'b'(c'+ c) = a'b' = (~a ^ ~b)
then negate (0 v 1 v 2 v 3)
~ (0 v 1 v 2 v 3)
= ~ (~ a ∧ ~ b)
= ~ (~ a) v ~ (~ b) ;;De Morgan’s: [DM] ∼(p ∧ q) ≡ (∼p) ∨ (∼q)
= a v b ;;Double Negation: [DNEG] ∼(∼p) ≡ p
in the rest options, (~ a ∧ b) v a is highly equivalent to (a v b), let's check
(~ a ∧ b) v a
=a v (~a ∧ b) ;;commutativity
=(a v ~a) ∧ (a v b) ;;distribution
=T ∧ (a v b) ;;Negation: [NEG] p ∨ (∼p) ≡ T
=a v b ;;Identity: [I] p ∧ T ≡ p
-
Q6. 2018S/slides/121-03-cond-equiv-ckh4up.pdf:page45 MUX Glitches
A Multiplexer is a circuit that, given three inputs a, b, and c (the “control” signal), outputs a’s value when c is 0 and b’s when c is 1. We can come up with a true table and logic expression

simplify the expression
(~a ∧ b ∧ c) v ( a ∧~b ∧ ~c) v ( a ∧ b ∧ ~c) v ( a ∧ b ∧ c)
=a'bc + ab'c' + abc' + abc
=(ab'c' + abc') + (a'bc + abc)
=ac'(b' + b) + bc(a' + a)
=ac' + bc
= (a ∧ ~c) v (b ∧ c)
so we can build up a circuit by (a ∧ ~c) v (b ∧ c)

MUX Glitches problem


How to fix?

proof (a ∧ b ) v ( a ∧ ~c) v ( b ∧ c) = ( a ∧ ~c) v ( b ∧ c)
(a ∧ b ) v ( a ∧ ~c) v ( b ∧ c)
=ab + ac' + bc
=ab(c + c') + ac' + bc
=abc + abc' + ac' + bc
=(abc + bc) + (abc' + ac')
=bc(a + 1) + ac'(b + 1)
=bc + ac' = ac' + bc
=(a ∧ ~c) v (b ∧ c)
-
Q7 Conditionals and Logical Equivalences
Consider: The Java [String] equals() method returns true if and only if the argument is not null and is a String object that represents the same sequence of characters as this object. Let
n1: the string is null
n2: the argument is null
nt: the method returns true
s: the two objects are strings that represent the same sequence of characters.
Is the sentence logically equivalent to "nt ↔ (n1 ^ n2) v s"? Why or why not?
The answer would be no. What consider said is "nt ↔ ~n2 ∧ s"
~n2 ∧ s is not equal to (n1 ^ n2) v s.
For example, if string and argument are both null, n1 is true and n2 is true.
Then ~n2 ∧ s is false, but (n1 ^ n2) v s is true.
-
Q8 Conditionals and Logical Equivalences
Consider the following code, part of a“binary bounds search”:
if target equals value then
if lean-left-mode is true
call the go-left routine
otherwise
call the go-right routine
otherwise if target is less than value then
call the go-left routine
otherwise
call the go-right routine
Let gl mean “the go-left() routine is called”. Complete the following: gl ↔ ??
Then, Use your logic to simplify the pseudo code so it requires just one “if/otherwise”.
e: target equals value
lm: lean-left-mode is true
l: target is less than value then
gl ↔ (e ^ lm) v lm
if ((target equals value and lean-left-mode) or target is less than value)) then
call the go-left routine
otherwise
call the go-right routine
-
Q9 Conditionals and Logical Equivalences
Prove: (a ^ ~ b) v (~ a ^ b) ≡ (a v b) ^ ~ (a ^ b)
(a ^ ~ b) v (~ a ^ b)
=ab' + a'b
=ab' + F + a'b + F ;;Identity: p ∨ F ≡ p
=ab' + aa' + a'b + bb' ;;Negation: p ∧ (∼p) ≡ F
=(ab' + bb') '+ (aa' + a'b) ;;Commutative: p ∨ q ≡ q ∨ p
=b'(a + b) + a'(a + b) ;;Distributive: p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
=(a + b)(a' + b') ;;Distributive: p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
=(a + b)(ab)' ;;De Morgan’s: ∼(p ∧ q) ≡ (∼p) ∨ (∼q)
=(a v b) ^ ~ (a ^ b)
-
Q10 Conditionals and Logical Equivalences
Problem: Aliens hold the Earth hostage, and only you can save it by proving
(a -> b) ∧ ~ (b -> a) ≡ ~ a ∧ b
(a -> b) ∧ ~ (b -> a)
=(~a v b) ∧ ~ (~b v a);; Implication: p → q ≡∼p ∨ q
=(a' + b)(a + b')'
=(a' + b)(a'(b')') ;;De Morgan’s: ∼(p ∨ q) ≡ (∼p) ∧ (∼q)
=(a' + b)(a'b) ;;Double Negation: ∼(∼p) ≡ p
=(a'b)(a' + b) ;;Commutative: p ∧ q ≡ q ∧ p
=(a'ba') + (a'bb) ;;Distributive: p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
=(a'a'b) + (a'bb) ;;Commutative: p ∧ q ≡ q ∧ p
=(a'b) + (a'b) ;;Idempotent: p ∧ p ≡ p
=a'b ;;Idempotent: p v p ≡ p
=~a ∧ b